O Teorema de Tales é fundamental na Geometria, principalmente no estudo de segmentos proporcionais que são formados por retas paralelas cortadas por transversais. Vamos entender como utilizá-lo por meio de alguns exercícios práticos.
Exercício 1
Na figura, temos as retas r, s e t em paralelo, cortadas por duas transversais, u e v. A tarefa aqui é calcular o segmento x.
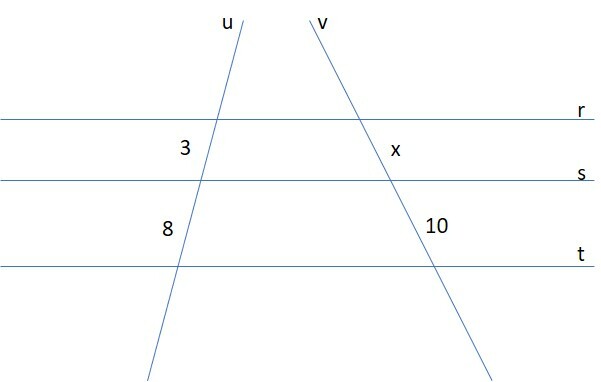
A resposta é explicada assim: de acordo com o Teorema de Tales, quando retas paralelas são cortadas por transversais, os segmentos resultantes nas transversais têm uma relação de proporção.
Neste caso, temos a relação:
[ \frac{3}{8} = \frac{x}{10} ]
Usando a regra das proporções, multiplicamos:
[ 8 \times x = 3 \times 10 ]
Assim, equilibrando a equação:
[ 8x = 30 ]
Resolvendo isso:
[ x = \frac{30}{8} ]
[ x = 3,75 ]
Portanto, a resposta correta é B) 3,75 cm.
Exercício 2
Aqui, apresentamos outra figura com as retas r, s e t paralelas. Esta questão pede para você descobrir os valores de x e y, sabendo que:
[ x + y = 12\,cm ]
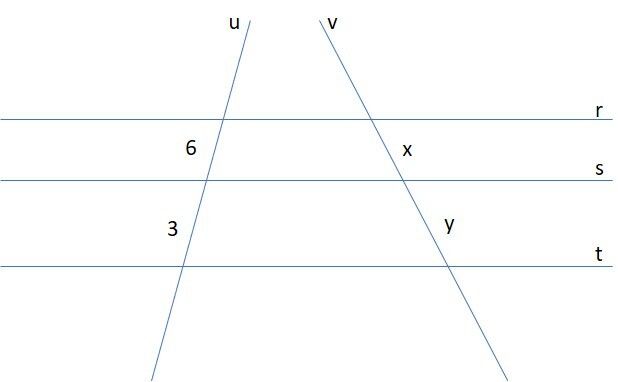
Para resolver, do Teorema de Tales, os segmentos criados pelas retas paralelas nas transversais também são proporcionais. Então, a proporção que podemos usar é:
[ \frac{6 + 3}{6} = \frac{x + y}{12} ]
Substituindo as variáveis:
[ \frac{9}{6} = \frac{12}{x} ]
[ 72 = 9x ]
[ x = 8\,cm ]
Agora, substituímos x na equação original:
[ y = 12 – x ]
[ y = 12 – 8 = 4\,cm ]
Assim, ficamos com x = 8 cm e y = 4 cm.
Exercício 3
Na figura, novamente, com as retas r, s e t paralelas, você tem os segmentos AB = 15 cm, BC = 10 cm e DE = 9 cm. A pergunta é: qual é o valor de EF?
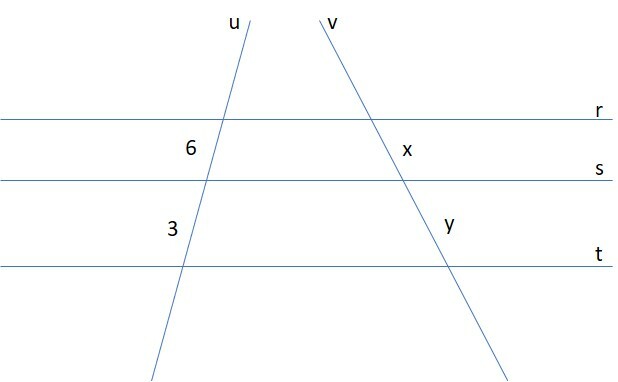
Aqui também aplicamos o Teorema de Tales. A proporção será:
[ \frac{AB}{BC} = \frac{DE}{EF} ]
Substituindo os valores que já conhecemos:
[ \frac{15}{10} = \frac{9}{EF} ]
Multiplicamos os valores cruzados:
[ 15 \cdot EF = 10 \cdot 9 ]
[ 15 \cdot EF = 90 ]
Resolvendo para EF:
[ EF = \frac{90}{15} ]
[ EF = 6\,cm ]
Assim, a resposta correta é C) 6 cm.
Exercício 4
Na última figura, temos quatro retas r, s, t e u em paralelo, sendo cortadas por duas transversais. A soma das medidas A + B + C é conhecida e dá 36 cm. A pergunta é encontrar os valores das medidas de A, B e C.
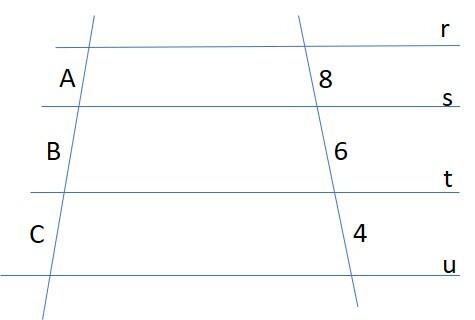
Para resolver isso, vamos utilizar novamente o Teorema de Tales. Ele diz que as retas paralelas formam segmentos proporcionais nas transversais. Para isso, começamos pelas proporções adequadas.
Escrevemos a primeira proporção. Usando o total de 36 cm em relação ao segmento A, devemos encontrar qual é a razão correspondente.
Vamos trabalhar com a primeira parte da equação. A razão desse segmento seria estabelecida em relação a 4 (soma de 8, 6 e 4).
[ \frac{A}{36} = \frac{4}{18} ]
Equilibrando a equação do segmento A:
[ A = \frac{36 \cdot 4}{18} ]
[ A = \frac{144}{18} ]
[ A = 8\,cm ]
Agora, encontramos B, utilizando:
[ \frac{B}{A} = \frac{6}{4} \to \frac{B}{8} = \frac{6}{4} ]
[ B = \frac{8 \cdot 6}{4} ]
[ B = 12\,cm ]
Agora vamos fazer A + B + C = 36 cm para achar C.
[ C = 36 – A – B = 36 – 8 – 12 = 16\,cm ]
Portanto, temos as medidas corretas, que são: A = 8 cm, B = 12 cm, C = 16 cm.
Considerações Finais
Esse conteúdo é uma ótima oportunidade para revisar o Teorema de Tales. Esse teorema é muito interessante e útil, pois nos ajuda a resolver diversos problemas de Geometria. Se você quiser continuar aprendendo, existem muitas outras matérias e teoremas relacionados à Matemática que podem ser explorados!
Assim, exploramos algumas aplicações práticas do Teorema de Tales. O ideal é praticar sempre para fixar o conhecimento. Mantenha-se sempre atualizado e curioso sobre a Matemática!

